All Real Numbers Are Solutions

Inequality with all real numbers equally solutions

An inequality with all real numbers as solutions is piece of cake to solve or piece of cake to recognize. See a few examples beneath.

Instance #1

Solve 10 - x > -1

x - 10 > -i

x - x = 0, so we become 0 > -1

Since 0 is ever bigger than -1, this inequality is always truthful. Therefore, all existent numbers are solutions.

Example #2

Solve 5x + ten + 3 > 6x + -4

5x + 10 + 3 > 6x + -iv

Subtract 3 from each side of the inequality

5x + 10 + 3 - 3 > 6x + -4 - iii

5x + x + 0 > 6x + -four + -3

5x + x > 6x + -7

Simplify by adding 5x and x

6x > 6x + -7

Subtract 6x from each side of the inequality

6x - 6x > 6x - 6x + -vii

0 > 0 + -7

0 > -7

Since 0 is e'er bigger than -7, this inequality is always true. Therefore, all existent numbers are solutions.

Chemical compound inequality with all existent numbers as solutions

Example #iii

Solve 8x + 4 ≤ 20 or 3x - ii > 1

Solve 8x + 4 ≤ twenty

8x + 4 ≤ 20

Subtract 4 from each side of the inequality

8x + 4 - 4 ≤ xx - 4

8x ≤ 16

Divide each side by 8

8x/8 ≤ 16/8

x ≤ 2

Solve 3x - two > i

3x - 2 > 1

Add 2 to each side of the inequality

3x - 2 + two > 1 + 2

3x - 2 + ii > 1 + 2

3x > 3

Split each side by 3

3x/3 > 3/3

x > i

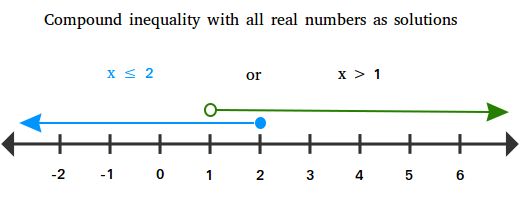
The solution is ten ≤ two or x > i and this includes all real numbers as shown in the graph below.

Compound inequality with all real numbers as solutions

Absolute value inequality with all real numbers as solutions

Example #4

Solve |x| > -x

The accented value of a number is e'er positive.

For example, suppose 10 is positive and choose x = 2

|2| = ii and 2 is e'er bigger -10

Suppose x is negative and choose x = -2

|-2| = 2 and 2 is always bigger than -10

Therefore, |ten| > -ten has all real numbers equally solutions

No affair what number you cull for ten, when you accept the absolute value, it will ever be bigger than -10.

In general, if |x| > a and a is a negative number, |ten| > a has all real numbers every bit solutions.